How relativity theory derived

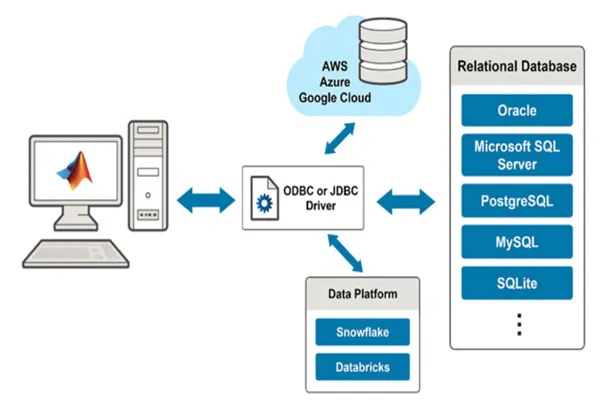
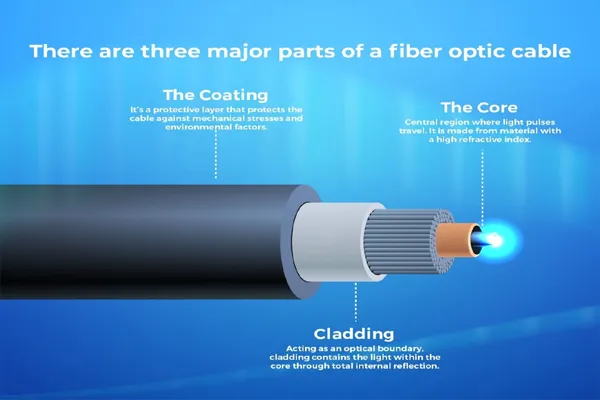
Let’s dive into how Einstein’s theory of relativity was derived, focusing on its two main forms: special relativity and general relativity. I’ll break it down step-by-step, keeping it clear and engaging, while sticking to the core ideas behind their development.

Special Relativity (1905)

Special relativity emerged from Einstein’s attempt to reconcile two seemingly incompatible pillars of physics: Newtonian mechanics and Maxwell’s equations for electromagnetism. Here’s how it came together:

The Problem: By the late 19th century, experiments like the Michelson-Morley experiment (1887) showed that the speed of light in a vacuum (about 299,792 km/s) was constant, regardless of the observer’s motion or the light source’s motion. This contradicted the Newtonian idea that velocities simply add up (e.g., if you’re on a train moving at 50 km/h and throw a ball at 10 km/h, the ball’s speed relative to the ground should be 60 km/h). Light didn’t behave this way—it always moved at the same speed, no matter what.
Einstein’s Insight: Instead of assuming there was some mysterious "aether" carrying light (a popular hypothesis at the time), Einstein took the constancy of light’s speed as a fundamental truth. In 1905, he published "On the Electrodynamics of Moving Bodies," proposing two postulates:
- Postulate 1: The laws of physics are the same in all inertial (non-accelerating) frames of reference.
- Postulate 2: The speed of light in a vacuum is constant and independent of the motion of the source or observer.
Derivation: From these postulates, Einstein used thought experiments and mathematics to explore the consequences. For example:
- Time Dilation: Imagine a "light clock" where a pulse of light bounces between two mirrors. For an observer at rest, the light travels straight up and down. For an observer moving relative to the clock, the light appears to take a longer, diagonal path. Since the speed of light is constant, the moving observer measures the time between ticks as longer than the stationary observer does. This leads to the equation: $t = \frac{t_{0}}{\sqrt{1 - v^{2} / c^{2}}}$ $t _{0}$ where $t_{0}$ $t_{0}$ is the time in the rest frame, $v$ $v$ is the relative velocity, and $c$ $c$ is the speed of light.
- Length Contraction: Similarly, objects moving relative to an observer appear shorter along the direction of motion: $L = L_{0} \sqrt{1 - v^{2} / c^{2}}$
- These effects, plus the relativity of simultaneity (events simultaneous in one frame may not be in another), required abandoning absolute time and space.
The Lorentz Transformation: Einstein adopted and refined equations from Hendrik Lorentz, which describe how space and time coordinates transform between inertial frames: $x^{'} = γ (x - v t), t^{'} = γ (t - v x / c^{2})$ $x^{'} = γ (x - v t), t^{'} = γ (t - vx / c^{2})$ where $γ = 1 / \sqrt{1 - v^{2} / c^{2}}$ . These replaced the simpler Galilean transformations of Newtonian physics.
E = mc²: As a bonus, special relativity showed that mass and energy are interchangeable. By analyzing the energy of moving objects and light emission, Einstein derived the famous equation: $E = m c^{2}$ $E = m c^{2}$ This emerged naturally from the relativistic treatment of momentum and energy.

Special relativity was a radical shift, built on simple postulates but backed by rigorous math and later confirmed by experiments (e.g., time dilation in particle accelerators).

General Relativity (1915)

General relativity extended special relativity to include gravity and accelerated motion. It took Einstein about a decade to develop, and here’s how he got there:

The Motivation: Special relativity worked for constant speeds, but gravity (still described by Newton’s inverse-square law) didn’t fit. Newton’s gravity acted instantaneously across distances, clashing with the finite speed of light limit.
The Equivalence Principle: Einstein’s big breakthrough came from a thought experiment: a person in a sealed, accelerating elevator feels a force indistinguishable from gravity. He proposed that:
- The effects of acceleration and gravity are equivalent (the equivalence principle).
- This suggested gravity isn’t a force in the traditional sense but a consequence of something deeper.
Geometry of Spacetime: Einstein realized that if gravity is tied to acceleration, it might bend the fabric of space and time. He turned to mathematics—specifically, Riemannian geometry—to describe this. With help from mathematician Marcel Grossmann, he learned about tensors and curvature. The key idea: mass and energy curve spacetime, and objects move along the "straightest" paths (geodesics) in this curved geometry.
Field Equations: After years of trial and error, Einstein formulated the Einstein Field Equations in 1915: $G_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν}$ $G_{μν} = c ^{4} 8 π G T_{μν}$
- $G_{\mu\nu}$ $G_{μν}$ : The Einstein tensor, describing spacetime curvature.
- $T_{\mu\nu}$ $T_{μν}$ : The stress-energy tensor, representing mass and energy.
- $G$ $G$ : Newton’s gravitational constant, $c$ $c$ : speed of light. This equation says that matter tells spacetime how to curve, and curved spacetime tells matter how to move.
Testing the Theory: Einstein derived predictions, like the bending of starlight near the Sun (confirmed in 1919 during a solar eclipse by Arthur Eddington) and the precession of Mercury’s orbit (a known anomaly Newton couldn’t explain). These successes cemented general relativity’s validity.

website

How relativity theory derived

Special Relativity (1905)

General Relativity (1915)

Related posts