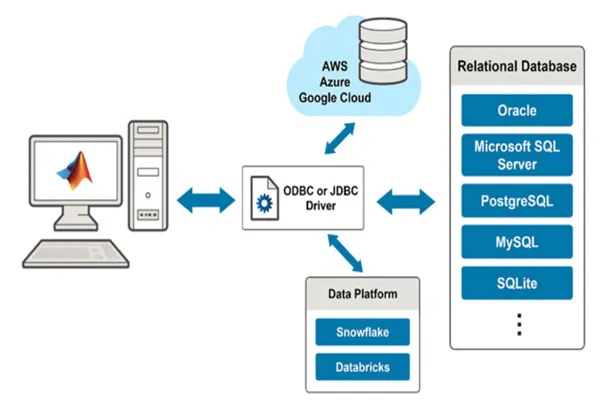
Velocity, as a vector quantity, describes the rate of change of an object’s position with both magnitude (speed) and direction
- Complete Description of Motion
- Advantage: Velocity is a vector quantity, incorporating both speed and direction, unlike speed, which is a scalar quantity. This allows for a more comprehensive understanding of an object’s motion. For example, knowing a car is moving at 60 km/h north provides critical directional information that speed alone (60 km/h) cannot convey.
- Application: This is essential in navigation, aerospace, and robotics, where direction is as crucial as magnitude. For instance, calculating the trajectory of a rocket requires precise velocity vectors to ensure it reaches its intended orbit.
- Enables Accurate Predictions
- Advantage: Velocity allows for precise predictions of an object’s future position, which is vital in fields like transportation and astrophysics. By knowing an object’s velocity, you can calculate when it will arrive at a destination.
- Example: If a train leaves a station at 2 p.m. with a velocity of 100 km/h north, you can predict its arrival time at a destination 200 km away (2 hours later, at 4 p.m.). This is used in creating timetables for travel.
- Foundation for Newton’s Laws and Mechanics
- Advantage: Velocity is integral to Newton’s laws of motion, particularly the first and second laws. The first law states that an object maintains constant velocity unless acted upon by a force, while the second law relates force to the rate of change of velocity (acceleration). This makes velocity a cornerstone of classical mechanics.
- Application: In engineering, velocity is used to design systems like vehicles or machinery, ensuring they operate within safe parameters by accounting for forces and motion.
- Differentiation Between Motion Types
- Advantage: Velocity distinguishes between linear and non-linear motion (e.g., circular motion). For example, in uniform circular motion, an object’s speed may remain constant, but its velocity changes due to the continuous change in direction, indicating acceleration. This distinction is critical for analyzing complex motions.
- Example: A car moving in a circular path at constant speed has changing velocity, which explains the centripetal force needed to keep it on the curve.
- Supports Conservation Laws
- Advantage: Velocity is key to defining momentum (mass × velocity), a conserved quantity in isolated systems. Using velocity as a vector ensures momentum conservation accounts for direction, making it more useful than a scalar-based definition.
- Example: In collisions, the vector nature of velocity ensures that momentum is conserved in each direction, allowing accurate predictions of post-collision motion.
- Facilitates Calculus-Based Analysis
- Advantage: Velocity is defined as the derivative of position with respect to time (v = ds/dt), enabling precise mathematical modeling of motion using calculus. The integral of velocity over time gives displacement, and the derivative of velocity gives acceleration.
- Application: This is crucial in physics and engineering for analyzing dynamic systems, such as calculating the trajectory of a projectile or the motion of planets.
- Practical Applications in Technology and Engineering
- Advantage: Velocity’s directional component is critical in fields like aerospace, automotive, and robotics. For example, in GPS navigation, velocity vectors help determine the precise path of a moving object. In robotics, velocity control ensures precise movements of robotic arms.
- Example: In aerospace engineering, velocity is used to calculate escape velocity, the speed needed to break free from a planet’s gravitational pull, which is vital for space missions.
- Enhances Safety and Efficiency
- Advantage: Understanding velocity helps design safer and more efficient systems. For instance, knowing a vehicle’s velocity allows engineers to calculate stopping distances or design airbag deployment systems based on changes in velocity (acceleration).
- Example: In automotive engineering, velocity data informs the design of anti-lock braking systems, ensuring vehicles stop efficiently without skidding.
- Supports Relativistic Physics
- Advantage: In special relativity, velocity is critical for understanding how objects behave at high speeds. The relativistic velocity-addition formula ensures that no object exceeds the speed of light, refining classical mechanics for high-speed scenarios.
- Application: This is used in particle physics and space exploration, where objects approach relativistic speeds, such as in particle accelerators or spacecraft traveling near light speed.
- Applications in Velocity-Based Training (VBT)
- Advantage: In sports science, velocity-based training uses velocity measurements to optimize strength training by providing real-time feedback on movement speed. This allows athletes to adjust intensity based on daily readiness, improving performance and reducing injury risk.
- Example: A powerlifter uses a VBT device to measure bar velocity during lifts, adjusting weight to maintain optimal training intensity.